- MATEMÁTICAS DISCRETAS I
- ROSANA GUTIERREZ MONTOYA
Trabajo Realizado Por:
Salinas Martinez Genny Guadalupe y Barajas Zepeda Sandra Lorena
UNIDAD 1
Sistemas Numericos
UNIDAD 2
Conjuntos
UNIDAD 3
Relaciones Y Funciones
UNIDAD 4
Logica Proposicional
UNIDAD 5
Algebra Booleana
UNIDAD 1
SISTEMAS NUMERICOS
- Binario
- Hexadecimal
- Romana
S.N - Arabigo
- Decimal
- Real o Fraccionario
- Maya
- Egipcio
1.-Definición de matemáticas discretas:
La matemática discreta es la parte de las matemáticas que estudia objetos discretos. Definir el concepto discreto sin entrar en demasiadas formalidades no es sencillo pero podemos apelar a ciertos ejemplos matemáticos conocidos y contraponerlo al concepto decontinuo que es la idea central del curso de Bases de Matemáticas. Lo discreto es lo finito o lo que, si no es finito, presenta el aspecto de los números naturales, objetos bien separados entre sí; lo continuo es lo no finito, lo infinitesimalmente próximo, como los números reales, y de ahí el concepto de límite y las ideas que de dicho concepto se derivan.
La matemática discreta surge como una disciplina que unifica diversas áreas tradicionales de las Matemáticas (combinatoria, probabilidad, geometría de polígonos, aritmética, grafos,...), como consecuencia de, entre otras cosas, su interés en la informática y las telecomunicaciones: la información se manipula y almacena en los ordenadores en forma discreta (palabras formadas por ceros y unos), se necesita contar objetos (unidades de memorias, unidades de tiempo), se precisa estudiar relaciones entre conjuntos finitos (búsquedas en bases de datos), es necesario analizar procesos que incluyan un número finito de pasos (algoritmos)...
primera fuente la encontré en www.escet.urjc.es/~matemati/md_iti/md_iti.html
Parte de la matemática que estudia los objetos Discretos (distintos o no conectados)
Son usadas en donde los objetos son contados, cuando las relaciones entre conjuntos finitos
son estudiados y cuando los procesos que involucran un numero finito de pasos son
analizados
segunda fuente la encontre en esintuitivo.blogspot.com/.../matemtica-discreta.html
Matemática discreta es la parte de la matemática encargada del estudio de losconjuntos discretos: finitos o infinitos numerables." bueno, es un poco redundante que una palabra se explique con la misma.
mas abajo:
"La matemática discreta estudia estructuras cuyos elementos pueden contarse uno por uno separadamente, sin dar lugar a números decimales ni procesos infinitos. Es decir, los procesos en matemática discreta son finitos y contables." Tal vez un poco mas claro para mí, pero no me aclara del todo el panorama. Esto es interesante: "la matemática discreta es la base de todo lo relacionado con los procesos digitales, y por tanto, se constituye en parte fundamental de la ciencia de la computación, una de las ramas de estudio impartidas en los estudios deIngeniería Informática." además de Ingeniería Informática, también Ingeniería en Software e Ingeniería en sistemas de Información.
Tercer fuente la encontré enesintuitivo.blogspot.com/.../matemtica-discreta.htm
Aplicaciones de matemáticas discretas, el uso de matemáticas discretas en la vida real. Una de las principales aplicaciones de las matemáticas discretas es en la informática y las telecomunicaciones: La información se manipula y almacena en los ordenadores en forma discreta (palabras formadas por ceros y unos), se necesita contar objetos (unidades de memorias, unidades de tiempo), se precisa estudiar relaciones entre conjuntos finitos (búsquedas en bases de datos), es necesario analizar procesos que incluyan un número finito de pasos (algoritmos).
http://www.buenastareas.com/ensayos/Matematicas-Discretas/281189.html
Matemática Discreta (Aritmética entera y modular y Teoría de Grafos). Los contenidos se han desarrollado tomando como eje central algunas de sus muchas aplicaciones a la Informática.
http://ocw.um.es/ingenierias/algebra-y-matematica-discreta
2.-DEFINICIÓN PROPIA:
M i definicion es que la matematicas discretas es parte de las matematicas que estudia objetos discretos surge como una disciplina que unifica diversas areas tradicionales de las matematicas
TAREA:
X0 = 1
X1 = X
X2 = X*X
X3 = X*X*X
3 8 510 2 3 58
/ / /---- 5 * 100 = 5 * 1 = 5 / / /----- 5 * 80 = 5 * 1 = 5
/ /---------8 * 101 = 8 * 10 = 80 / / ------------ 3* 81 = 3 * 8 = 2 4
/--------------3 * 10 = 3 * 100 = 300 /------------- 2 * 82 = 2 * 64 = 128
385 15710
1 3 46 1 0 4 3 4 2
/ / /----- 4 * 60 = 4 * 1 = 4 / / /-------- 4 * 50 = 4 * 1 = 4 / / /--- 2 * 7 = 2 * 1 = 2
/ /--------- 3 * 61 = 3 * 6 = 18 / /----------- 0 * 51 = 0 * 5 = 5 / /------- 4 * 7 = 4 * 7 = 28
/------------- 1 * 62 = 1 * 36 = 36 /----------------1 * 52 = 1 * 25= 25 /----------- 3 * 7 = 3 * 49= 147
5810 34 17710
- Convierta A Decimal Los Siguientes Números: Tarea 1
A) I00II = 130310 B) I0II00 = C) IIII0III = 247 D) I000000 = 64
E) II20II000II = 1635 F) III0IIII0= 478 G) I000I = 17 H) I00I000 = 72
i) II00I00II = 403 J) IIIIIIII = 255 k) II2I0 = L) III0III0II =
M) I0000 = 16 N) IIIII0I =125 Ñ) IIII0000=240
- Convierta A Octal Y Hexadecimal Los Siguientes Números Indicando La Separación De Los Bits: Tarea 2
A) III 0II ; II I0II B) I III I00 ; III II00 C) I0 0I0 I00 ; I00I 0I00
7 38 3 BH 1 7 48 7 CH 2 2 48 9 4H
E) I I0I 0I0 0I0 ; II 0I0I 00I0 F) II 00I ; I I00I G) I0 III 0I0 0II ; I0I II00 00II
1 5 2 28 3 5 2H 3 18 1 9H 2 7 2 38 5 D 3H
H) I 0II 0I0 0II ; I0 IIOI I00I i) I00 00I 0II ; I 0000 I0II J) I 0I0 II0 ; I0I 0II0
1 3 3 18 2 D 9H 4 1 38 1 0 BH 1 2 68 5 6H
K) III 0II 0I0 ; I II0I I0I0 L) I 0II 0II I0I ; I0 II0I II0I M) I 000 000 0I0 ; I0 0000 00I0
7 3 28 1 D AH 1 3 3 58 2 D DH 1 0 0 28 2 0 2H
Ñ) I0 II0 II0 0I0 ; I0I I0II 00I0
2 6 6 28 5 B 2H
Convierta A Octal Los Siguientes Hexadecimales Utiliza La Conversión Binaria
- AÑO
Base 8 Base 2
1990 / 3706 3 7 0 6
-------------- / / / /
248 / 6 011 111 000 110
31/ 0
3/ 7
base 7 base 16
1990 / 5542 0111 1100 0110
-------------- / ----------/ /-------/ /---------/2
284/ 2 7 C 6H
40/ 4
5/ 5
base 4
1990 / 133012
-----------------
497 / 2
124/1
31/ 0
7/3
1/3
- NUMERO DE CONTROL
base 8 base 2
0607 / 211334 1 1 3 7
--------------- / / / /
75 / 7 001 001 011 111 2
9 / 3
1 / 1
base 7 base 4 base 16
0607 / 1525 0607 / 21133 0010 0101 1111
---------------- --------------- / / /
86 / 5 151 / 3 2H 5 F
12 / 2 37 / 3
1 / 5 9 / 1
2 / 1
base 8 base2
7 1
3706 1137 11111000110 01001011111
1137 6640 1001011111 10110100000
------- 1 ---------------- 1
2547 ---------- 10101100111 ------------------
2547 10110100001
111111000110
-------------------
10101100111
base 7 base 16
6 15 25F
5542 1525 7C6 25F 567
1525 5141 25F DA0 -----
------ -------- ------- 1 7C6
4041 4014 547 --------
DA1
1525 7C6
4014 ------
----- 567
5542
base 4
3 133012
021133 133012 332121
133012 200321 ---------
--------- 1 021133
332121 ------------
200322
021133
-----------
332121
- Clasifique las siguientes expresiones del idioma en proposiciones lógicas,proposiciones abiertas o expresiones indeterminadas.
1.- Colon descubrió américa en miércoles.
proposicion logica
2.- 2 + 2 = 5.
proposicion logica
3.- Espérame un momento.
frase
4.- Estudien mucho.
frase
5.- X + 1< 4.
proposición abierta
6.- Estoy mintiendo
proposición abierta
7.- Todos los pericos son verdes.
proposición lógica
8.- La mesa es de color rojo.
proposición lógica
9.- Un angulo recto mide 90 Grados.
proposición lógica
- Niegue las expresiones siguientes
10.- Algunos peces pueden nadar
Algunos peces no pueden nadar
11.- El agua es transparente
el agua no es transparente
12.- México esta en américa
mexico no esta en america
13.- La mesa es azul
la mesa no es azul
14.- Todos los días hace calor
todos los dias no hace calor
15.- Ningun oso polar tiene frio
algun oso polar no tiene frio
16.-Algun sabio toma cafe
algun sabio no toma cafe
- Escriba las siguentes expresiones en forma simbolica
17.- Hoy es lunes o mañana sera sabado
18.- Un numero distinto de cero es positivo o negativo
19.- Si no llueve iremos de dia de campo
20.- Se pueden estacionar algunos maestros
21.- Si encuentra un producto mejor, comprelo
22.- El no es rico, ni feliz
23.-Ser pobre es ser feliz
24.- Hay que saber matematicas para ser feliz
- Escriba con palabras las siguientes expresiones simbolicas.
25.-
SISTEMA OCTAL:
0,1,2,3,4,5,6,7 dígito mayor mayor(base 1). conversión automática octal
O | 0001 |
1 | 0001 |
2 | 0010 |
3 | 0011 |
4 | 0100 |
5 | 0101 |
6 | 0110 |
7 | 0111 |
8 | 1000 |
9 | 1001 |
A | 1010 |
B | 1011 |
C | 1100 |
D | 1101 |
E | 1110 |
F | 1111 |
- LÓGICA PROPOSICIONAL
Para este ejemplo de álgebra de Boole el conjunto B es el conjunto de todos los enunciados
gramaticales. La operación suma (+) es la conjunción gramatical “o” (OR), la multiplicación es la conjunción gramatical “y” (AND) y los valores que puede tomar un enunciado gramatical son {falso,verdadero} = {F,V}.
En la siguiente figura se muestra un ejemplo en donde se aclara de manera precisa el sentido de las operaciones OR y AND (ya que puede ser diferente de la interpretación gramatical cotidiana), para ello se introduce el concepto de tabla de verdad, la cual es simplemente una tabulación de los enunciados y todas las posibles combinaciones de sus correspondientes valores de verdad o falsedad.
Ejemplo. Consideremos los siguientes los enunciados:
x = "Todo ingeniero electricista domina la Transformada de Fourier"
y = "Todo ingeniero electricista conoce las normas ISO-9000"
suma lógica:
x+y = x o y = “Todo ingeniero electricista domina la Transformada de Fourier o conoce las normas
IS0-9000"
producto lógico:
x y = x y y = "Todo ingeniero electricista domina la transformada de Fourier y conoce las normas ISO-9000"
complemento:
x = no x = "no todo ingeniero electricista domina la transformada de Fourier" =”existe al menos un ingeniero electricista que no domina la transformada de Fourier” ¹ “ningún ingeniero electricista domina la transformada de Fourier”
Tablas de verdad:
x y x+y x y x y x y
F F F F F F F V
F V V F V F V F
V F V V F F
V V V V V V
Ejemplo de un Neutro de la suma:
F = "Todo ingeniero electricista es premio novel de literatura'
Ejemplo de un Neutro de la multiplicación:
V = "Todo ingeniero electricista es mayor de edad"
- Existencia de neutros. El neutro de la suma, es un enunciado que evidentemente siempre es falso,
(ver ejemplo). en forma similar, el neutro de la multiplicación es un enunciado que evidentemente siempre
es verdadero.
3.- Conmutatividad. Evidentemente las conjunciones “y”, “o” no alteran el sentido del enunciado total,
independientemente del orden en que son tomados.
4.- Asociatividad. Las conjunciones “y”, “o” son asociativas, es decir, al conectar tres enunciados
gramaticales con “y” o con “o” no importa cual par de enunciados evaluemos primero para determinar si
el enunciado total es verdadero o falso.
5.- Distributividad. La conjunción “y” es distributiva sobre la conjunción “o” y viceversa, esto es fácil de
probar mediante tablas de verdad, como se muestra a continuación:
x y z x y x z x y + x z y+z x (y+z)
F F F F F F F F F F
F F V F F F V F V F
F V F F F F V F V F
F V V F F F V F V F
V F F F F F F F F F
V F V F V V V V V V
V V F V F V V V V V
V V V V V V V V V V
- ALGEBRA BOOLEANA
UNIDAD 5
Álgebra de Boole (también llamada Retículas booleanas) en informática y matemática, es una estructura algebraica que rigorizan las operaciones lógicas Y, O y NO, así como el conjunto de operaciones unión, intersección y complemento.
Se denomina así en honor a George Boole, (2 de noviembre de 1815 a 8 de diciembre de 1864), matemático inglés que fue el primero en definirla como parte de un sistema lógico a mediados del siglo XIX. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional. En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948.
- DEFINICION
Una álgebra de Boole es una tripleta  . Donde
. Donde  , + y
, + y  son operaciones internas en
son operaciones internas en  y además para cualquier
y además para cualquier  se cumplen los siguientes axiomas:
se cumplen los siguientes axiomas:
 . Donde
. Donde  , + y
, + y  son operaciones internas en
son operaciones internas en  y además para cualquier
y además para cualquier  se cumplen los siguientes axiomas:
se cumplen los siguientes axiomas:1. Propiedad conmutativa:
2. Propiedad asociativa:
3. Propiedad distributiva:
4. Propiedad de los neutros. Existen  tales que:
tales que:
 tales que:
tales que:5. Propiedad de los opuestos. Existe  tal que:
tal que:
 tal que:
tal que:
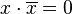
Como retículo
Como retículo presenta las siguientes propiedades, las leyes principales son estas:1. Ley de Idempotencia:2. Ley de Asociatividad:3. Ley de Conmutatividad:4. Ley de Cancelativo

- OPERACIONES
Hemos definido el conjunto A = {1,0} como el conjunto universal sobre el que se aplica el álgebra de Boole, sobre estos elementos se definen varias operaciones, veamos las más fundamentales:Operación suma
a b a + b 0 0 0 0 1 1 1 0 1 1 1 1 La operación suma (+) asigna a cada par de valores a, b de A un valor c de A:Su equivalencia en lógica de interruptores es un circuito de dos interruptores en paralelo.Si uno de los valores de a o b es 1, el resultado será 1, es necesario que los dos sumandos sean 0, para que el resultado sea 0.
Estosresultados son presentados a manera de Teoremas y junto con los seis postulados representan las reglas del juego para cualquiera que desee trabajar con el álgebra booleana. La manera de demostrar los teoremas siguientes se puede basar en ideas intuitivas producto de la familiaridad con algún álgebra booleana en particular, (en diagramas de Venn, o bien, en circuitos con switches o en tablas de verdad) con la única condición de que se respete al pie de la letra los 6 postulados fundamentales. En estas notas sólo se usan razonamientos basados en los seis postulados. Antes de presentar los teoremas es conveniente mencionar el siguiente principio que se deriva directamente de la manera en que fueron presentados los seis postulados fundamentales, es decir, del hecho de que cada postulado tiene dos incisos los cuales son duales uno del otro. Principio de Dualidad. Si una expresión booleana es verdadera, su expresión dual también lo es. Expresiones duales. Dos expresiones se dicen duales una de la otra, si una se puede obtener de la otra cambiando las operaciones ( + ) por ( ) y viceversa y cambiando los O's por 1 's y viceversa.Ejemplo.La expresión A + B = 1 es dual de la expresión A B = O,Todas las expresiones de los incisos (a) de los postulados del álgebra booleana son duales de lasexprsiones de los incisos (b) correspondientes.Teorema 1. Multiplicación por ceroa) A 0 = 0b) A+1 = 1Demostración del inciso (a)Explicación:A 0 = A 0 + 0 0 es el neutro de la suma= A 0 + A A el producto de una variable por su complemento da 0= A (0 + A) distributividad= A (A) una variable más el neutro no se altera
Notación. De aquí en adelante, el símbolo de multiplicación ( ) se omitirá en ocaciones por comodidad, así por ejemplo A B se escribirá AB, o bien, (A+B) (C+D) se escribirá (A+B)(C+D) siendo diferente de A+B C+D, lo cual se escribirá A+BC+D.
Teorema 2. Absorcióna) A + AB = Ab) A(A + B) = A
Demostrando el inciso (a)Explicación:A + AB = A 1 + AB 1 es el neutro del producto= A(1 + B) distributividad= A(1) Teorema 1= A es el neutro del productoeste teorema se puede usar en diversos casos de simplificación, basta con usar identificar en una suma,una expresión que se repite primero en forma aislada y luego multiplicando a otra expresión.Ejemplos.La expresión XY + XYZ por absorción es igual a XYLa expresión A+ AB por absorción es igual con Aetc.Teorema 3. Cancelacióna) A + AB = A + Bb) A(A + B) = A BDemostración del inciso (a)Explicación:A + AB = (A+A)(A+B) distributividad= 1 (A+B) la suma de una variable con su complemento es 1= A+B 1 es el neutro del ProductoEste teorema se puede usar en la simplificación de expresiones cuando encontramos una expresiónsumada Con su complemento multiplicado por otra expresión (o el dual).Ejemplos:La expresión A + ABC por cancelación es igual a A + BCLa expresión A + AB por cancelación es igual a A + BLa expresión XY + XY Z por cancelación es igual a XY + ZTeorema 4. Cancelacióna) AB + AB = Bb) (A+B)(A+B)=BDemostración del inciso (a)Explicación:AB + A B = (A+A )B distributividad= 1 B la suma de una variable con su complemento es 1= B 1 es el neutro del productoPara usar este resultado hay que identificar dos términos que tienen un factor común y el término que noes común en una de ellas es el complemento del de la otra.Ejemplos:La expresión ABC+ABC, por cancelación es igual a BCLa expresión XYZ+XY Z, por cancelación es igual a ZTeorema 5. Idempotenciaa) A A = Ab\ A+A= A
La demostración del inciso (b) de este teorema es inmediata del teorema de absorción, ya que A + A =A+ A 1.Este teorema implica que cuando existen términos semejantes en una expresión, basta con escribir unode ellos, o bien, que un término puede "desdoblarse" tantas veces como se quiera. Obsérvese quetambién esto implica que An= A para cualquier número n entero positivo.Ejemplos:La expresión (X+Y)(X+Y) por idempotencia es igual a X+YLa expresión XYZXYX por idempotencia es igual a XYZLa expresión XY+Z+ XY por idempotencia es igual a XY+ZTeorema 6. Consensoa) AB + AC + BC = AB + ACb) (A+B)(A+C)(B+C) = (A+B)( A+C)Demostración del inciso (a)Explicación:AB +AC + BC = AB +AC + BC(A +A) A+A es el neutro de la multiplicación= AB +AC +ABC +ABC distributividad= (AB +ABC) + AC +ABC) conmutatividad y asociatividad= AB + AC absorciónLa clave para usar este teorema es encontrar dos términos que contengan una expresión en uno afirmada y en otro negada, anotar los términos con los que están multiplicando uno y otro y buscar otro elemento que sea la multiplicación de estos últimos dos, éste último elemento es el que se puede eliminar.Ejemplos:La expresión AB + AC + BC por consenso es igual a AB + ACLa expresión XYZ + XY W + ZW por consenso es igual a XYZ + XY WTeorema 7. Teorema de De Morgana) AB = A+Bb) A+B = ABDemostración del inciso (a): Para demostrar este teorema hay que recordar las dos propiedades quecumple el complemento X de una expresión X, es decir:i) X + X = 1 (sumados nos da uno)ii) X X = 0 (multiplicados nos da cero)Así, para demostrar el inciso (a) se demostrará que A+B es el complemento de A.B, para ello se hará endos partes:i) sumando:Explicación:AB + (A + B ) = AB + B + A por conmutatividad= A + B + A por cancelación= 1 + B propiedad del complemento= 1 por Teorema 1ii) multiplicandoExplicación:A B (A + B ) = ABA + ABB Por distributividad= 0 + 0 propiedad del complemento= 0 idempotenciaEl teorema de De Morgan se puede generalizar al caso de más de dos variables booleanas, por ejemplo,para 3 variables, tenemos que A+B+C = (A+B )C = A B C, en forma similar, AüBüC = (AüB )+C =A +B +C , y así sucesivamente para más de tres variables.Otros teoremas: A continuación se presentan dos teoremas más sin demostración, es un buen ejercicioel intentar dicha demostración.Teorema 8. Involucióna) A =ATeorema 9. Complementos de los neutrosa) 0 = 1b) 1 = 04.3.1.- Ejemplos de simplificación de expresiones booleanasLos 6 postulados fundamentales, junto con los teoremas anteriores conforman las herramientas básicasde simplificación y manipulación de expresiones booleanas, a continuación se ilustra su uso con algunosejemplos.Ejemplo. Simplificar las siguientes expresiones1.- A(BC + AC) + BC Distribuyendo el factor A en el paréntesis:= ABC + AAC + BC, conmutando y aplicando idempotencia:= ABC + BC + AC, usando absorción:= BC +AC2.- XYZ+XZ Usando el Teorema de De Morgan:= XYZüXZ , por De Morgan nuevamente e involución:= (XY+Z )( X +Z ), distribuyendo:=XYX +XYZ +X Z +Z Z , como X X es cero, y por idempotencia:= 0+ XYZ +X Z +Z , por absorción:= Z3.- (X+Y+YZW)XY Por el teorema de De Morgan:= ((X+Y) YZW) XY, nuevamente:= (X+Y) (Y+Z+W) (X+Y) , distribuyendo el primero con el tercer factor:= (XY+XY) (Y+Z+W) , distribuyendo nuevamente= (XY+XYZ+XYW+XYZ+XYW, por absorción:=(XY+XYZ+XYW).4.4.- FUNCIONES BOOLEANASEn forma similar a como se define en los cursos de álgebra de números reales, es posible definir unarelación de dependencia de una variable booleana o variable lógica con otras variables booleanasindependientes. Es decir, es posible definir funciones booleanas o funciones lógicas.Definición. Sean X1,X2,...,Xn, variables booleanas, es decir, variables que pueden tomar el valor de 0 ode 1, entonces la expresiónY = f(X1,X2,...,Xn)denota una dependencia funcional de la variable dependiente Y respecto a las variables independientesX1,X2,...,Xn, es decir, el valor (0 o 1) que toma la variable Y depende de la combinación de n valores (1’s y0’s) que tomen las n variables X1,X2,...,Xn.Ejemplo: La siguiente es una función booleanaY= f(A,B,C) = AB + A C + ACEsta función se puede evaluar para diversos valores de sus variables independientes A, B, C:Si A = 1, B = 0, C = 0 entonces Y= f(1,0,0) = 1.0 + 0.0 + 1.1 = 1,Si A = 1, B = 1, C = 0 entonces Y= f(1,1,0) = 1.1 + 0.0 + 1.1 = 1,Si A = 0, B = 1, C = 0 entonces Y= f(0,1,0) = 0.1 + 1.0 + 0.1 = 0, etc.A diferencia de las funciones de variable real, las cuales no pueden representarse completamenteusando una tabla de valores, las funciones booleanas sí quedan totalmente especificadas por unatabla que incluya todas las posibles combinaciones de valores que pueden tomar las variablesindependientes, dicha tabla se denomina tabla de verdad y es completamente equivalente a la expresiónbooleana, ya que incluye todas sus posibilidades.Ejemplo. La siguiente es la tabla de verdad para la función del ejemplo anteriorA B C f(A,B,C)0 0 0 00 0 1 10 1 0 00 1 1 11 0 0 11 0 1 01 1 0 11 1 1 1En general para una función de n variables, puesto que hay n variables y cada variable tiene dos posiblesvalores, hay 2nmaneras de asignar estos valores a las n variables, así la tabla de verdad tendrá 2nrenglones.Por ejemplo en el ejemplo anterior f(A,B,C) es una función de 3 variables, por lo que tenemos 23= 8diferentes combinaciones de las entradas y por lo tanto 8 renglones de la tabla de verdad.4.4.1.- FUNCIONES BOOLEANAS DE UNA y DOS VARIABLESEn el caso de funciones de variable real sería imposible tratar de mencionar todas las posibles funcionesde una o más variables, sin embargo, en el caso de funciones booleanas se puede hacer un listadocompleto de todas y cada una de las funciones para cierto número de variables. a continuación se haceuna lista de éstas para los casos de 0, 1 y 2 variables independientes:Funciones de cero variables. Estas son las funciones constantes y sólo hay dos:f0 = 0 Función constante cerof1 = 1 Función constante unoFunciones de una variable. Además de las funciones constantes ahora se pueden definir otras dos:f0(A) = 0 Función constante cerof1(A) = A Función identidadf2(A) = A Función complemento, negaciónf3(A) = 1 Función constante unoFunciones de dos variables. En este caso se pueden definir 16 funciones diferentes, las cuales incluyen las cuatro anteriores y otras doce más. En las siguiente tabla se muestra un resumen de las dieciséisfunciones de dos variables, incluyendo su nombre, su tabla de verdad, y su expresión lógica (booleana).Const.CERO AND Identidad Identidad EXOR ORA B 0 A B A B A A B B A Å B A + B0 0 0 0 0 0 0 0 0 00 1 0 0 0 0 1 1 1 11 0 0 0 1 1 0 0 1 11 1 0 1 0 1 0 1 0 1NOREQUIVALENCIA NOT NOT NANDConst.UNOA B A+ B A ? B B A+ B A A+ B A B 10 0 1 1 1 1 1 1 1 10 1 0 0 0 0 1 1 1 11 0 0 0 1 1 0 0 1 11 1 0 1 0 1 0 1 0 1OBSERVACIÓN. Ciertamente, las expresiones lógicas que aparecen en la tabla anterior no sonúnicas, ya que una misma función lógica puede tener diferentes representaciones algebraicas.Ejemplo: Es fácil ver queA B = AB + AB = (A + B)(A + B)o bien, también por ejemploA ? B = A B = AB + AB = (A + B)(A + B).etc ...A continuación se presenta una alternativa gráfica para trabajar en el análisis y diseño de funcionesbooleanas a partir de bloques funcionales que se representan mediante símbolos lógicos.4.4.2. SÍMBOLOS DE PUERTAS LÓGICASUna manera generalizada de representar las funciones lógicas es el uso de símbolos o bloques lógicosdenominados puertas o compuertas lógicas. Estas puertas en general representan bloques funcionalesque reciben un conjunto de entradas (variables independientes) y producen una salida (variable dependiente) como se muestra en la figura siguiente.
Una de las ventaja de usar éstos símbolos es que por ser una representación entrada / salida permiten la “interconexión” de puertas (la salida de una con la entrada de otra) para representar funciones más complejas a partir de funciones sencillas. Otra ventaja es el hecho de que los bloques sencillos (puertas con pocas entradas) se encuentran disponibles en circuitos integrados comerciales, de aquí que un diagrama de puertas lógicas corresponde directamente a un diagrama de alambrado de circuito lógico.



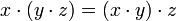

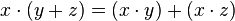



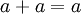
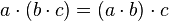
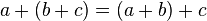
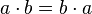
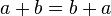


No hay comentarios:
Publicar un comentario